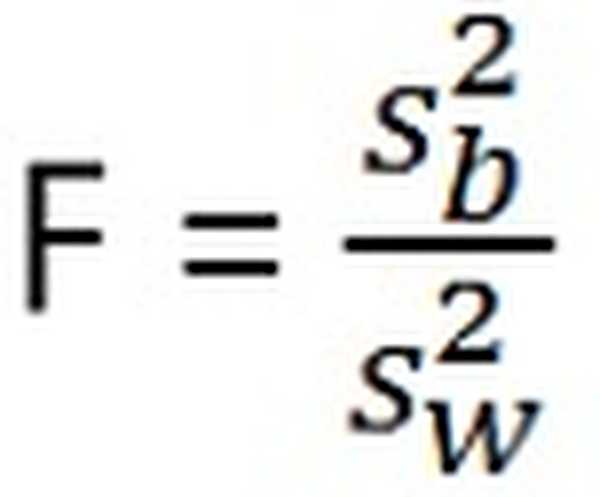Skirtumas tarp T-testo ir ANOVA
 Share
Share
 Tarp t-testo ir ANOVA yra plona demarkacijos linija, t. Y. Kai reikia palyginti tik dviejų grupių populiacijų vidurkius, t-testas yra naudojamas, bet kai reikia palyginti daugiau nei dviejų grupių vidurkius, ANOVA yra teikiama pirmenybė.
Tarp t-testo ir ANOVA yra plona demarkacijos linija, t. Y. Kai reikia palyginti tik dviejų grupių populiacijų vidurkius, t-testas yra naudojamas, bet kai reikia palyginti daugiau nei dviejų grupių vidurkius, ANOVA yra teikiama pirmenybė.
T-testas ir variacijos analizė, sutrumpintai vadinama ANOVA, yra du parametriniai statistiniai metodai, naudojami hipotezei patikrinti. Kadangi jos grindžiamos bendra prielaida, kaip paprastai turėtų būti paskirstoma imties populiacija, dispersijos homogeniškumas, atsitiktinė duomenų atranka, stebėjimų nepriklausomumas, priklausomo kintamojo matavimas santykiu ar intervalo lygiu, žmonės dažnai klaidingai juos interpretuoja. du.
Štai jums pateiktas straipsnis, kad suprastumėte reikšmingą skirtumą tarp t-testo ir ANOVA, pasižiūrėkite.
Turinys: T-testas vs ANOVA
- Palyginimo diagrama
- Apibrėžimas
- Pagrindiniai skirtumai
- Išvada
Palyginimo diagrama
| Palyginimo pagrindas | T testas | ANOVA |
|---|---|---|
| Reikšmė | T-testas yra hipotezės testas, naudojamas palyginti dviejų populiacijų vidurkius. | ANOVA yra statistinis metodas, naudojamas palyginti daugiau nei dviejų populiacijų vidurkius. |
| Testo statistika | (x ̄-µ) / (s / √n) | Tarp mėginio dispersijos / mėginio variacijos |
T-testo apibrėžimas
T-testas apibūdinamas kaip statistinis testas, kurio metu tiriama, ar dviejų mėginių populiacijos vidurkis labai skiriasi viena nuo kitos, naudojant t-pasiskirstymą, kuris naudojamas, kai standartinis nuokrypis nežinomas, o imties dydis yra mažas. Tai įrankis analizuoti, ar du mėginiai yra paimti iš tos pačios populiacijos.
Testas grindžiamas t-statistika, kuri daro prielaidą, kad kintamasis paprastai pasiskirsto (simetriškas varpo formos pasiskirstymas), o vidurkis žinomas, o populiacijos dispersija apskaičiuojama pagal imtį.
„T-test“ nulinė hipotezė įgauna H formą0: µ (x) = µ (y) pagal alternatyvią hipotezę H1: µ (x) ≠ µ (y), kur µ (x) ir µ (y) žymi populiacijos vidurkį. T-testo laisvės laipsnis yra n1 + n2 - 2
ANOVA apibrėžimas
Variacijos analizė (ANOVA) yra statistinis metodas, paprastai naudojamas visose situacijose, kai reikia palyginti daugiau nei dvi populiacijos priemones, pavyzdžiui, derliaus derlių iš kelių sėklų veislių. Tai yra gyvybiškai svarbi tyrėjo analizės priemonė, leidžianti jam vienu metu atlikti testą. Kai mes naudojame ANOVA, daroma prielaida, kad mėginys imamas iš normaliai pasiskirstančios populiacijos ir populiacijos dispersija yra lygi.
ANOVA duomenų rinkinyje visas variacijos dydis yra padalijamas į dvi rūšis, ty suma, paskirta atsitiktinumui, ir suma, paskirta tam tikroms priežastims. Pagrindinis jo principas yra išbandyti skirtumus tarp populiacijos priemonių, įvertinant variacijų dydį grupės elementuose, proporcingą variacijų dydžiui tarp grupių. Imties dispersija atsiranda dėl atsitiktinai nepaaiškinamų trikdžių, tuo tarpu mėginio dispersija gali būti skirtinga.
Taikant šią metodiką, mes patikriname niekinę hipotezę (H0), kur visos populiacijos priemonės yra vienodos, arba alternatyvi hipotezė (H1) kurioje bent vienos populiacijos vidurkis yra skirtingas.
Pagrindiniai skirtumai tarp T-testo ir ANOVA
Svarbūs T-testo ir ANOVA skirtumai išsamiai aptariami šiuose punktuose:
- Hipotezės testas, kuris naudojamas palyginti dviejų populiacijų vidurkius, vadinamas t-testu. Statistinė metodika, naudojama palyginti daugiau nei dviejų populiacijų vidurkius, yra žinoma kaip dispersijos analizė arba ANOVA.
- T-testo bandymo statistika yra:
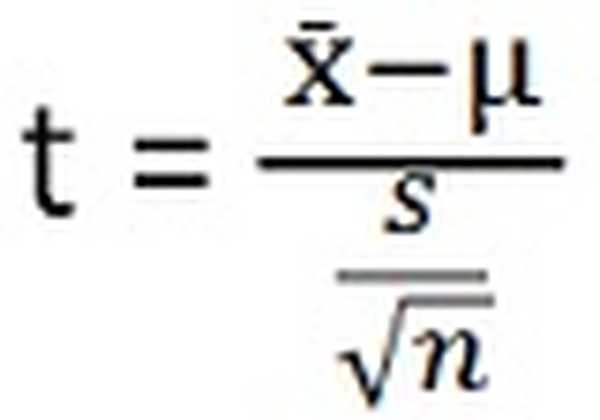 ANOVA bandymo statistika yra:
ANOVA bandymo statistika yra: 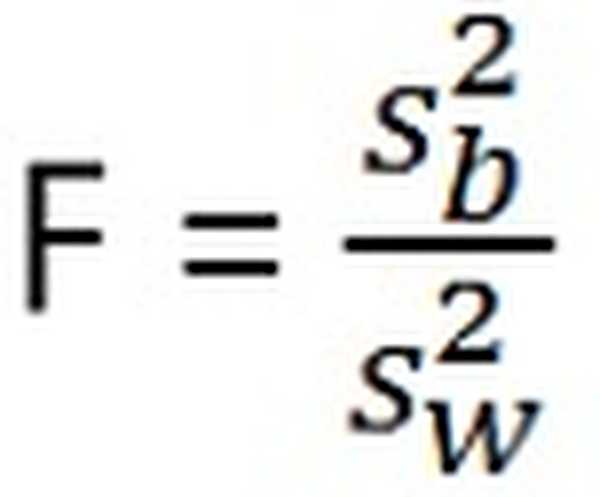
Išvada
Peržiūrėjus aukščiau pateiktus punktus, galima pasakyti, kad t-testas yra ypatingas ANOVA tipas, kuris gali būti naudojamas, kai turime tik dvi populiacijas, kad palygintume jų vidurkius. Nors klaidų tikimybė gali padidėti, jei naudojamas t-testas, kai vienu metu turime palyginti daugiau nei dvi populiacijų vidutines reikšmes, todėl naudojama ANOVA
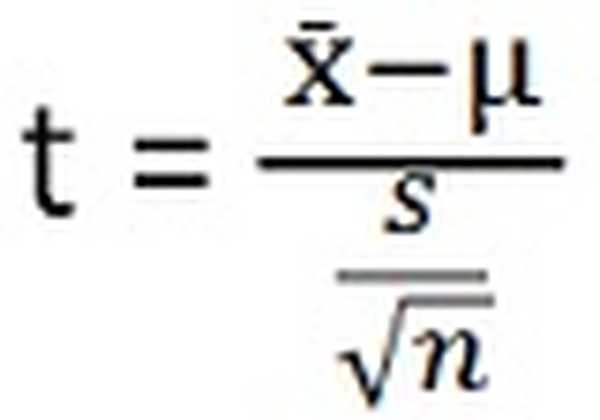 ANOVA bandymo statistika yra:
ANOVA bandymo statistika yra: